Teorema de Pitágoras

Baseado em conhecimentos geométricos adquiridos com agrimensores egípcios, Pitágoras percebeu uma relação muito importante ao construir um quadrado sobre cada um dos lados de um triângulo retângulo de lados 3, 4 e 5.

            Observe que o quadrado construído sobre a hipotenusa tem tantos quadradinhos quanto os quadrados construídos sobre os catetos.

Daí, Pitágoras obteve a relação:

25 = 9 + 16     =>        5² = 3² + 4²

 

Abaixo você encontra uma lista de aplicativos e simuladores sobre o Teorema de Pitágoras. Acesse e se divirta aprendendo matemática!

 

Soma dos Quadrados dos catetos

Este applet java mostra um triângulo retângulo. Podes mover o vértice do ângulo reto. Para acessar este applet clique aqui.

 

 

 

 

Quando se desconhece a hipotenusa

Resolver problemas com triângulos retângulos, quando a hipotenusa é desconhecida. Para acessar este objeto de aprendizagem clique aqui.

 

 

Triângulo de Pitágoras

 Objetivo:

Aprender o Teorema de Pitágoras

Resumo:

Para acessar este aplicativo clique aqui.

·         O teorema de Pitágoras aplica-se a todos os triângulos retângulos

·         Este teorema diz que, num triângulo retângulo, em que a hipotenusa é c, c² = a² + b², ou seja, “o quadrado da hipotenusa é igual à soma dos quadrados dos catetos”.

 

 

Identificar quando pode ser utilizado o Teorema de Pitágoras

Para acessar este aplicativo clique aqui.

 

Aplicação do Teorema de Pitágoras

Objetivo: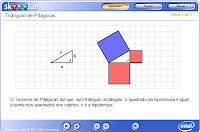

Para acessar este aplicativo clique aqui.

Aprender e resolver problemas envolvendo o Teorema de Pitágoras

Resumo:

·         O Teorema de Pitágoras aplica-se a todos os triângulos retângulos.

·         Este teorema diz que num triângulo retângulo em que a hipotenusa é C e os catetos são A e B, então C² = A² + B².

·         Teorema é recíproco. Ou seja, se um triângulo obedece ao Teorema de Pitágoras, então esse triângulo é retângulo, isto é, tem um ângulo reto.

 

 

Teorema de Pitágoras – Altura dos Prédios

Objetivo da simulação: Aprender o Teorema de Pitágoras.

Clique aqui para acessar este aplicativo.

O teorema de Pitágoras diz que, num triângulo retângulo, o quadrado da hipotenusa (o lado maior) é igual à soma dos quadrados dos catetos (os outros dois lados).

  

 

Explorador do Teorema de Pitágoras

Agora chegou o momento de você exercitar tudo o que você aprendeu sobre Teorema de Pitágoras. Clique aqui para realizar as atividades propostas neste explorador.